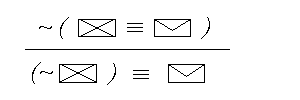
---- Księga Gości ----
Wpisz się... | Przeglądaj...
5.
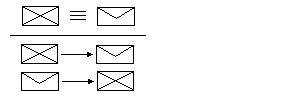
SYSTEM ZALOZENIOWY RACHUNKU ZDAN
- jest to kolejna, po matrycowej, metoda
przeprowadzania rachunku zdan, polegajaca na
dowodzeniu tautologicznosci schematu,
wylacznie poprzez ustalone reguly (dyrektywy) dowodzenia (wnioskowania). Tych reguł jest ich co prawda
mnostwo, aczkolwiek podam Ci je w na tyle
przystepny sposob, ze po niewielkim uplywie
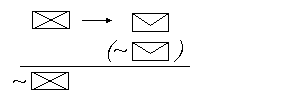
czasu zapewne beda one Twoje: 1. REGULA
ODRYWANIA - jesli do dowodu naleza dwie
rzeczy : pierwsza - implikacja i druga - jej
poprzednik, wystepujacy samodzielnie, to
wolno nam oderwac ten poprzednik z
implikacji, pozostawiajac jedynie sam
nastepnik .
UWAGA ! Czasem pojawia sie
w zadaniach koniunkcja skladajaca sie z
wiecej niz dwoch czesci, np. p
Wariant II
Wariant III
Wariant IV
Wariant V
Wariant VI
WARIANT II
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
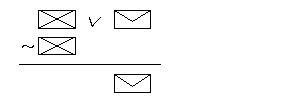
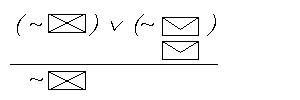
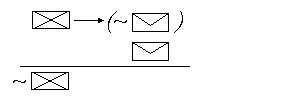
Budujac zalozeniowy dowod wprost schematu o postaci: W1
Od razu przyklad:
(p

Mamy wiec schemat : “(p
- jak wyczytalismy to w powyzszej definicji, musimy zaczac od wypisania zalozen, czego poprawne wykonanie jest polowa naszego sukcesu:
| 1. p 2. r 3. p |
zal. zal. zal. |
Widzisz, ze mamy teraz trzy zalozenia : I - jest nim ZAWSZE wszystko to, co wystepuje przed glowna implikacja calego schematu (wyrazenie : “p II - jest nim ZAWSZE wszystko to, co wystepuje przed glowna implikacja nastepnika calego schematu (wyrazenie : “r III - jest nim ZAWSZE wszystko to, co wystepuje przed ostatnia implikacja, jaka mamy w schemacie (wyrazenie : “p”, u nas to pole adresowe prawej wielkiej koperty , a w definicji figurujace jako “Wn”). - kolejny krok to dokonanie stosownych przeksztalcen na podstawie znanych regul: |
|
| 4. r 5. q |
RO : 1,3 RO : 2,4 |
UWAGA ! Trzeba koniecznie zapisywac ktore wiersze biora udzial w danej regule i tak np. w naszej RO uzytej w wierszu 4 braly udzial : wiersz 1 i 3 . PAMIETAJ! W wierszu czwartym zastosowalismy znana nam reg. odrywania, uzywajac do tego celu rzeczy z wiersza pierwszego i trzeciego: 1. p ... 3. p 4. r W wierszu piatym zastosowalismy takze RO: 2. r ... 4. r 5. q - tak oto dostalismy, co chcielismy: nasz piaty wiersz jest zgodny z rzecza, ktora mielismy osiagnac, czyli ZAWSZE tym, co znajduje sie po ostatnim znaku implikacji wystepujacym w calym schemacie (wyrazenie : “q”, u nas jest to znaczek przyklejony na prawej wielkiej kopercie, a w definicji figurujace jako “W”). - pozostaje teraz jedynie napisac odpowiedz, ze badany schemat jest tautologia. Zapis calego dzialania wyglada nastepujaco : (p |
| 1. p |
zal. |
| 2. r |
zal. |
| 3. p | zal. |
| 4. r | RO : 1,3 |
| 5. q Odp. Ten schemat jest tautologia. |
RO : 2,4 |
|
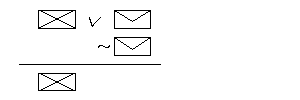
| 1. p 2. r 3. p |
zal. zal. zal. |
Sa w tym przypadku trzy zalozenia: I - jest nim ZAWSZE wszystko to, co wystepuje przed glowna implikacja calego schematu (wyrazenie : “p II - jest nim ZAWSZE wszystko to, co wystepuje przed glowna implikacja nastepnika calego schematu (wyrazenie : “r III - jest nim ZAWSZE wszystko to, co wystepuje przed ostatnia implikacja, jaka mamy w schemacie (wyrazenie : “p”, u nas to pole adresowe prawej wielkiej koperty , a w definicji figurujace jako “Wn”). - teraz musimy dodac tzw. “zalozenie dowodu niewprost”, ktore to ZAWSZE jest NEGACJA tego wyrazenia, ktore znajduje sie po ostatnim znaku implikacji wystepujacym w calym schemacie (wyrazenie : “q”, u nas jest to znaczek przyklejony na prawej wielkiej kopercie, a w definicji figurujace jako “W”). Cala sprawa wyglada tak : |
|
| 4. ~ q | z.d.n. (UWAGA!“z.d.n.”trzeba tutaj pisac PAMIETAJ!) |
| - dalszy krok - przeksztalcenia na podstawie regul: | |
| 5. r 6. ~ r |
RO : 1,3 MT : 2,4 |
| Wiersz nr 6 wzial sie stad: 2. r ... 4. ~ q ... 6. ~ r |
|
| - i naszym oczom
ukazala sie upragniona sprzecznosc :
wyrazenie w wierszu piatym jest sprzeczne z
wyrazeniem z wiersza szostego, co pozwala
nam udzielic odpowiedzi, iz schemat jest
tautologia. UWAGA! Nie musimy wcale szukac negacji wyrazenia, ktore wystepuje po ostatniej implikacji - “znaczka”, by uzyskac sprzecznosc, a tym samym udowodnic tautologicznosc schematu. Wystarczy, jak ma to miejsce w podanym tu przykladzie, ze znajdziemy jakakolwiek sprzecznosc. PAMIETAJ!. Zapis calego dzialania wyglada nastepujaco: (p |
|
| 1. p |
zal. |
| 2. r |
zal. |
| 3. p | zal. |
| 4. ~ q | z.d.n. |
| 5. r | RO : 1,3 |
| 6. ~ r Odp. Sprzecznosc:5,6 - schemat jest tautologia. |
MT : 2,4 |
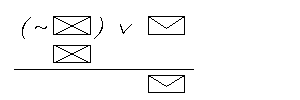
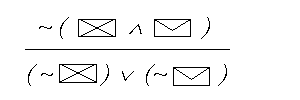
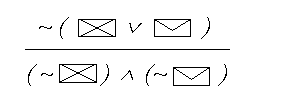
UWAGA ! Dowodzenie tautologicznosci schematu, ktorego glownym spojnikiem nie jest implikacja najlepiej robic metoda “NIEWPROST”. Oto kolejne kroki tej procedury w przypadku takiego rodzaju schematu (glownym spojnikiem jest tu alternatywa): ( p  (calosc traktujemy
sobie jako swoisty nastepnik nieistniejacej
w istocie implikacji) (calosc traktujemy
sobie jako swoisty nastepnik nieistniejacej
w istocie implikacji)- ZAWSZE zaczynamy wiec od “zalozenia dowodu niewprost” - zanegowania calego schematu (u nas jest to cala koperta), gdyz nigdy nie wypisuje sie zwyklych zalozen (taki panuje tu konwenans): |
|
| 1. ~ [( p |
z.d.n. |
| - przeksztalcenia, zgodne ze
znanymi regulami: |
|
| 2. ~ ( p |
NA : 1 |
| 3.~ ( p |
OK : 2 |
| 4. ~ ( q |
OK : 2 |
| 5. p |
NI : 3 |
| 6. q |
NI : 4 |
| 7. p | OK : 5 |
| 8. ~ q | OK : 5 |
| 9. q | OK : 6 |
| 10. ~ p | OK : 6 |
- pokazala sie "jakakolwiek" sprzecznosc (wiersze: 8,9 , a nawet dodatkowo wiersze : 7,10 , choc wystarczylaby zupelnie jedna, ale “od przybytku sprzecznosci glowa nie boli”), co sklania nas do odpowiedzi, iz badany schemat jest tautologia. PAMIETAJ ! Zapis calego dzialania wyglada nastepujaco : ( p |
|
| 1. ~ [( p |
z.d.n. |
| 2. ~ ( p |
NA : 1 |
| 3.~ ( p |
OK : 2 |
| 4. ~ ( q |
OK : 2 |
| 5. p |
NI : 3 |
| 6. q |
NI : 4 |
| 7. p | OK : 5 |
| 8. ~ q | OK : 5 |
| 9. q | OK : 6 |
| 10. ~ p Odp. Sprzecznosc: 8,9 - schemat jest tautologia. |
OK : 6 |
|
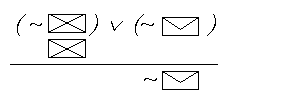
c) ZALOZENIOWE DOWODZENIE
ROZGALEZIONE - jest to
specyficzny rodzaj prowadzenia procesu
sprawdzania tau- |
| 1. ( p V q ) 2. ~ [( p 3. ~ ( p |
zal. z.d.n. NK : 2 |
- nie dajemy za wygrana, pomimo wyczerpania znanych dotad nam form konwersji naszego schematu, i robimy taki oto “zwod”: Rozbijamy ALTERNATYWE z wiersza nr 3 na dwa zalozenia dodatkowe: |
| 1.1. ~ ( p |
z.d. | 2.1. ~ ( q |
z.d. |
| (Literki : “z.d.” musza zostac umieszczone w tych miejscach) |
- dokonujemy przeksztalcen, wykorzystujac do tego celu wszystkie dostepne dotychczas wiersze (UWAGA ! W kolumnie lewej, zaczynajacej sie od wiersza nr 1.1. NIE WOLNO wykorzystywac rzeczy z kolumny prawej, zaczynajacej sie od wiersza nr 2.1. ; i na odwrot : w kolumnie prawej, zaczynajacej sie od wiersza nr 2.1. NIE WOLNO wykorzystywac rzeczy z kolumny lewej, zaczynajacej sie od wiersza nr 1.1. PAMIETAJ!): |
| 1.2. p |
NI : 1.1. | 2.2. q |
NI : 2.1. |
| 1.3. p | OK : 1.2. | 2.3. q | OK : 2.2. |
| 1.4. ~ r | OK : 1.2. | 2.4. ~ r | OK : 2.2. |
| 1.5. ~ (p V q) | MT : 1, 1.4. | 2.5. ~ (p V q) | MT : 1, 2.4. |
| 1.6. ~ p |
NA : 1.5 | 2.6. ~ p |
NA : 2.5 |
| 1.7. ~ p | OK : 1.6. | 2.7. ~ p | OK : 2.6. |
| 1.8. ~ q | OK : 1.6. | 2.8. ~ q | OK : 2.6. |
- i znajdujemy w ten sposob sprzecznosci pomiedzy jakimikolwiek wyrazeniami, pamietajac, ze pierwsza musimy uzyskac w lewej kolumnie (TYLKO wiersze z tej kolumny biora udzial w jej formowaniu), druga zas w prawej kolumnie (TYLKO wiersze tej kolumny biora udzial w jej formowaniu): |
| Sprzecznosc : 1.3. ; 1.7. | Sprzecznosc : 2.3. ; 2.8. |
Ostatecznie, po odnalezieniu obu sprzecznosci, dajemy odpowiedz, ze nasz schemat jest tautologia. Podsumowujac, dzialania nasze powinny zostac zapisane w nastepujacy sposob: [( p V q ) |
| 1. ( p V q ) |
zal. |
| 2. ~ [( p |
z.d.n. |
| 3. ~ ( p |
NK : 2 |
| 1.1. ~ ( p |
z.d. |
2.1. ~ ( q |
z.d. |
| 1.2. p |
NI : 1.1. | 2.2. q |
NI : 2.1. |
| 1.3. p | OK : 1.2. | 2.3. q | OK : 2.2. |
| 1.4. ~ r | OK : 1.2. | 2.4. ~ r | OK : 2.2. |
| 1.5. ~ (p V q) | MT : 1, 1.4. | 2.5. ~ (p V q) | MT : 1, 2.4. |
| 1.6. ~ p |
NA : 1.5 | 2.6. ~ p |
NA : 2.5 |
| 1.7. ~ p | OK : 1.6. | 2.7. ~ p | OK : 2.6. |
| 1.8. ~ q Sprzecznosc : 1.3. ; 1.7. |
OK : 1.6. | 2.8. ~ q Sprzecznosc : 2.3. ; 2.8. |
OK : 2.6. |
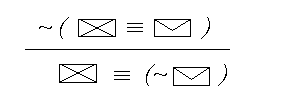
Odp. Ten schemat jest tautologia. => DOWOD ROZGALEZIONY “WPROST” Tym razem mamy taki oto schemat: ( p  - wypisujemy zalozenia i dokonujemy mozliwych przeksztalcen : |
| 1. p 2. p V r |
zal. zal. |
- znow wyczerpalismy znane dotad formy konwersji naszego schematu (poniewaz koniecznie postanowilismy utrudnic sobie zycie i przeprowadzic dowodzenie metoda wprost), wiec rozbijamy ALTERNATYWE na dwie kolumny zalozen dodatkowych: |
| .1. p | z.d. | 2.1. r | z.d. |
| - dokonujemy przeksztalcen, wykorzystujac do tego celu wszystkie dostepne dotychczas wiersze (UWAGA! Tu takze w kolumnie lewej, zaczynajacej sie od wiersza nr 1.1. NIE WOLNO wykorzystywac rzeczy z kolumny prawej, zaczynajacej sie od wiersza nr 2.1. ; i na odwrot : w kolumnie prawej, zaczynajacej sie od wiersza nr 2.1. NIE WOLNO wykorzystywac rzeczy z kolumny lewej, zaczynajacej sie od wiersza nr 1.1. PAMIETAJ!): |
| 1.2. q 1.3. q V r |
RO : 1, 1.1. DA : 1.2. |
2.2. q V r | DA : 2.1. |
(Wolno nam dodawac jakiekolwiek wyrazenie, tworzac w ten sposob w nowym wierszu prawdziwa alternatywe, jesli wiemy, ze jeden z jej elementow - ten, ktory mielismy juz w dowodzie, jest prawdziwy - ma wartosc logiczna 1. BTW - to przypadek, ze w lewej kolumnie musielismy wykorzystac litere “r”, wystepujaca w prawej kolumnie oraz w prawej litere “q”, wystepujaca w lewej, aby uzyskac alternatywe . W przypadku reguly DA nie obowiazuje nas zasada niewykorzystywania w jednej z kolumn zalozen dodatkowych rzeczy pochodzacych z drugiej kolumny.) - i tworzymy w ten sposob w obu kolumnach to wyrazenie, ktore wystepuje po ostatnim znaku implikacji (u nas “q V r” - to znaczek prawej koperty). - ostatecznie piszemy odpowiedz, ze nasz schemat jest tautologia. Wszystko powinno byc zapisane w taki sposob: ( p |
| 1. p 2. p V r |
zal. zal. |
| 1.1. p 1.2. q 1.3. q V r |
z.d. RO : 1, 1.1. DA : 1.2. |
2.1. r 2.2. q V r |
z.d. DA : 2.1. |
Odp. Ten schemat jest tautologia. Dla wprawy zbadajmy sobie jeden taki schemacik : ( p |
| 1.(p |
zal. | ||
| 2. ~ ~ ( p |
z.d.n. | ||
| 3. p |
ON : 2 | ||
| 1.1. p |
z.d. |
2.1. ~ p |
z.d. |
| 1.2. p |
OK : 1.1. | 2.2. ~ p | OK : 2.1. |
| 1.3. ~ q | OK : 1.1. | 2.3. q | OK : 2.1. |
| 1.4. p |
OR : 3 | 2.4. p |
OR : 3 |
| 1.5. q |
OR : 3 | 2.5. q |
OR : 3 |
| 1.6. ~ p Sprzecznosc : 1.2. ; 1.6. Odp. To jest tautologia. |
MT : 1.3. ; 1.4. | 2.6. p Sprzecznosc : 2.2. ; 2.6. |
RO : 2.3. ; 2.5. |
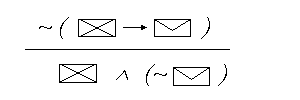
Sprawdzimy teraz nasze umiejetnosci w polu dowodzenia tautologii metoda wprost:
a) [( p

| 1. ( p |
zal. |
(cala lewa koperta) |
| 2. p | zal. | (znaczek "AIR MAIL" na prawej) |
| 3. q | zal. | (pole adresowe na prawej) |
| 4. p |
DK : 2,3 | |
| 5. r | RO : 1,4 | (otrzymalismy znaczek z prawej) |
Odp. Ten schemat jest tautologia. _____ b) [ p  |
||
| 1. p |
zal. |
(cala lewa koperta) |
| 2. p |
zal. | (pole adresowe prawej koperty) |
| 3. p | OK : 2 | (“rozlozylismy” koniunkcje |
| 4. q | OK : 2 | z drugiego wiersza) |
| 5. q |
RO : 1, 3 | (sam nastepnik z pierwszego wiersza) |
| 6. r | RO : 4,5 | (mamy znaczek prawej koperty) |
Odp. Ten schemat jest tautologia. _____ c) [(p  |
| 1. (p |
zal. |
(lewa koperta) |
| 2. p |
zal. |
(pole adresowe prawej) |
| 3. p |
OK : 1 | |
| 4. p |
OK : 1 |
|
| 5. q |
RO : 2,3 |
|
| 6. r |
RO : 2,4 |
|
| 7. q |
DK : 5,6 | (znaczek prawej koperty) |
Odp. Ten schemat jest tautologia. _____ d) [q  |
| 1. q |
zal. |
(lewa koperta) |
| 2. q |
zal. | (pole adresowe prawej) |
| 3. q | OK : 1 | |
| 4. p |
OK : 1 | |
| 5. q | OK : 2 | |
| 6. p | OK : 2 | |
| 7. r | RO : 4,6 | (znaczek prawej koperty) |
| Odp. Ten schemat jest tautologia. _____ e) ~ (~ p  |
| 1. ~ (~ p |
zal. |
(lewa koperta) |
| 2. p | zal. | (pole adresowe prawej) |
| 3. ~ p |
NI : 1 | |
| 4. ~ p | OK : 3 | |
| 5. ~ ~ q | OK : 3 | |
| 6. q | ON : 5 | (znaczek prawej koperty) |
Odp. Ten schemat to tautologia. CWICZENIE 10 Utrwalimy teraz zyskane umiejetnosci w dowodzeniu niewprost aby “zaznac poczucia wlasnej mocy logicznej” przed czekajacymi nas kolejnymi wyzwaniami w tym polu: a) ( ~ q  |
| 1. ~ q |
zal. |
(nasza lewa koperta) |
| 2. p | zal. | (pole adresowe prawej koperty) |
| 3. ~ q | z.d.n. | (negacja znaczka prawej koperty) |
| 4. ~ p | RO : 1,3 | |
Odp. Sprzecznosc: 2,4 - schemat ten jest tautologia. _____ b) ( ~ q V p )  |
||
| 1. ~ q V p |
zal. |
(nasza lewa koperta) |
| 2. q | zal. | (pole adresowe prawej koperty) |
| 3. ~ p | z.d.n. | (negacja znaczka prawej koperty) |
| 4. p | OA : 1,2 | |
Odp. Sprzecznosc: 3,4 - schemat ten to tautologia. _____ c) [ (p  |
||
| 1. (p |
zal. |
(lewa koperta) |
| 2. p |
zal. | (pole adresowe) |
| 3. ~ ~ q | z.d.n. | (zanegowany znaczek) |
| 4. q | ON : 3 | |
| 5. p | OK : 2 | |
| 6. ~ r | OK : 2 | |
| 7. p |
DK : 4,5 | |
| 8. r | RO : 1,7 | |
Odp. Sprzecznosc: 6,8 - schemat jest tautologia. _____ d) [(p  |
||
| 1. (p |
zal. | (lewa koperta) |
| 2. p |
zal. | (pole adresowe) |
| 3. ~ r | z.d.n. | (zanegowany znaczek) |
| 4. p | OK : 2 | |
| 5. q | OK : 2 | |
| 6. p |
DK : 3,4 |
|
| 7. ~ q | RO : 1,6 | |
Odp.Tautologia - sprzecznosc: 5,7 CWICZENIE 11 Kilka schemacikow do przerobki umyslowej (dowodzenie tautologicznosci schematow, gdzie glowny spojnik to nie implikacja): a) ~ ( p |
| 1. ~ ~ ( p |
z.d.n. |
| 2. p |
ON : 1 |
| 3. p | OK : 2 |
| 4. ~ p Odp. Sprzecznosc:3,4 - ten schemat to tautologia. _____ |
OK : 2 |
| b) ( ~ p |
|
| 1. ~ [( ~ p |
z.d.n. |
| 2. ~ ( ~ p |
NA : 1 |
| 3. ~ ( ~ p |
OK : 2 |
| 4. ~ ~ ( p |
OK : 2 |
| 5. ~ p |
NI : 3 |
| 6. p |
ON : 4 |
| 7. ~ p | OK : 5 |
| 8. ~ q | OK : 5 |
| 9. p | OK : 6 |
| 10. r Odp. Sprzecznosc: 7,9 - schemat to tautologia. _____ |
OK : 6 |
| c) ( ~ p |
|
| 1. ~ [( ~ p |
z.d.n. |
| 2. ~ ( ~ p |
NA:1 |
| 3. ~ ( ~ p |
OK : 2 |
| 4. ~ ( p V ~ r ) |
OK : 2 |
| 5. ~ p |
NI : 3 |
| 6. ~ p |
NA : 4 |
| 7. ~ p |
OK : 5 |
| 8. ~ q |
OK : 5 |
| 9. ~ p |
OK : 6 |
| 10. ~ ~ r |
OK : 6 |
| 11. r Odp. Sprzecznosci brak = 0 tautologii... _____ |
ON : 10 |
| d) (p |
|
| 1. ~ {(p |
z.d.n. |
| 2. ~ (p |
NA : 1 |
| 3. ~ (p |
OK : 2 |
| 4. ~ [( p |
OK : 2 |
| 5. ~ ( p |
NR : 4 |
| 6. ~ ( p |
OR : 5 |
| 7. ( q |
OR : 5 |
| 8. q |
RO : 3,6 |
| 9. q | OK : 8 |
| 10. p | OK : 8 |
| 11. ~ p V ~ q | NK : 3 |
| 12. ~ p Odp. Sprzecznosc:10,12 - schemat jest tautologia. |
OA : 9,11 |
CWICZENIE 12 To bedzie jedno z najobszerniejszych cwiczen tej e-ksiazki, gdyz dowodzenie tautologicznosci metodami zalozeniowymi wprost i niewprost “jest tym, co Logicy lubia najbardziej”: |
| a) [q |
|
| 1. q |
zal. |
| 2. p | zal. |
| 3. q | OK : 1 |
| 4. p |
OK : 1 |
| 5. r | RO : 2,4 |
| 6. q Odp. Ten schemat jest tautologia. _____ |
DK : 3,5 |
| b) ~ { [ ( p |
|
| 1. ~ ~ { [ ( p |
z.d.n. |
| 2. [ ( p |
ON : 1 |
| 3.( p |
OK : 2 |
| 4. r |
OK : 2 |
| 5. p |
OK : 3 |
| 6. q | OK : 3 |
| 7. r |
OK : 4 |
| 8. ~ q Odp. Sprzecznosc : 6,8 - schemat to tautologia. _____ |
OK : 4 |
| c) [ r |
|
| 1. r |
zal. |
| 2. ~ (~ p |
z.d.n. |
| 3. r |
OK : 1 |
| 4. p |
OK : 1 |
| 5. ~ p |
NI : 2 |
| 6. ~ p |
OK : 5 |
| 7. ~ ~ q |
OK : 5 |
| 8. q |
ON : 7 |
| 9. p |
OR : 4 |
| 10. q |
OR : 4 |
| 11. p Odp. Sprzecznosc: 6,11 - schemat to tautologia. _____ |
RO : 8,10 |
| d) [p |
|
| 1. p |
zal. |
| 2. ~ r |
zal. |
| 3. ~ r | OK : 2 |
| 4. p | OK : 2 |
| 5. ~ ( q V s ) | RO : 1,4 |
| 6. ~ q |
NA : 5 |
| 7. ~ q | OK : 6 |
| 8. ~ s Odp. Ten schemat jest tautologia. _____ |
OK : 6 |
| e) [(p |
|
| 1. (p |
zal. |
| 2. ~ ~ p | z.d.n. |
| 3. p | ON : 2 |
| 4. p |
OK : 1 |
| 5. ~ q | OK : 1 |
| 6. ~ p Odp. Sprzecznosc:3,6 - schemat jest tautologia. _____ |
MT : 4,5 |
| f) ~ ~ {[ p |
|
| 1. ~ ~ {[ p |
zal. |
| 2. ~ [ ~ q V ( p |
z.d.n. |
| 3. [ p |
ON : 1 |
| 4. ~ ~ q |
NA : 2 |
| 5. ~ ~ q | OK : 4 |
| 6. ~ ( p |
OK : 4 |
| 7. [ p |
OR : 3 |
| 8. ~ q |
OR : 3 |
| 9. q | ON : 5 |
| 10. ~ [ p |
MT : 7,9 |
| 11. p |
NI : 6 |
| 12. p | OK : 11 |
| 13. ~ ~ s | OK : 11 |
| 14. s | ON : 13 |
| 15. p |
NI : 10 |
| 16. p | OK : 15 |
| 17. ~ ( r V s ) | OK : 15 |
| 18. ~ r |
NA : 17 |
| 19. ~ r | OK : 18 |
| 20. ~ s Odp. Sprzecznosc: 14,20 - schemat to tautologia. _____ |
OK : 18 |
| g) ( ~ p |
|
| 1. ~ p |
zal. |
| 2. ~ ~ ( p V q ) | z.d.n. |
| 3. ~ p | OK : 1 |
| 4. ~ q | OK : 1 |
| 5. p V q | ON : 2 |
| 6. p Odp. Sprzecznosc: 3,6- ten schemat to tautologia. _____ |
OA : 4,5 |
| h) [ p |
|
| 1. p |
zal. |
| 2. p |
zal. |
| 3. ~ (p |
z.d.n. |
| 4. p |
NI : 3 |
| 5. p | OK : 4 |
| 6. ~ r | OK : 4 |
| 7. q |
RO : 1,5 |
| 8. q | OK: 7 |
| 9. r Odp. Sprzecznosc: 6,9 - schemat to tautologia. _____ |
OK: 7 |
| i) (~p |
|
| 1.~ p |
zal. |
| 2. ~ [( p V r ) V ( q V r )] | z.d.n. |
| 3. ~ ( p V r ) |
NA : 2 |
| 4.~ ( p V r ) | OK : 3 |
| 5. ~ (q V r ) | OK : 3 |
| 6. ~ q |
NA : 5 |
| 7. ~ q | OK : 6 |
| 8. ~ r | OK : 6 |
| 9. ~ ~ p | MT : 1,7 |
| 10. p | ON : 9 |
| 11.~ p |
NA : 4 |
| 12. ~ p Odp. Sprzecznosc : 10, 12 - tautologia. _____ |
OK : 11 |
| j) [~ (p |
|
| 1. ~ (p |
zal. |
| 2. ~ (p V s) | zal. |
| 3. ~ (p |
OK : 1 |
| 4. r |
OK : 1 |
| 5.~ p |
NA : 2 |
| 6. p |
NI : 3 |
| 7. ~ p | OK : 5 |
| 8. ~ s | OK : 5 |
| 9. p | OK : 6 |
| 10. ~ q | OK : 6 |
| 11. ~ r | MT : 4,8 |
| 12. p Odp. Schemat tautologiczny. _____ |
DK : 9,11 |
| k) [~ (p |
|
| 1.~ {[~ (p |
z.d.n. |
| 2.~ [~ (p |
NA : 1 |
| 3. ~ [~ (p |
OK : 2 |
| 4. ~ [~ p |
OK : 2 |
| 5. ~ ~ (p |
NA : 3 |
| 6. ~ ~ p V ~ ( q |
NK : 4 |
| 7. ~ ~ (p |
OK : 5 |
| 8. ~ ( r |
OK : 5 |
| 9. p |
ON : 7 |
| 10. r |
NI : 8 |
| 11. p |
OR : 9 |
| 12. q |
OR : 9 |
| 13. r |
OK : 10 |
| 14. ~ p |
OK : 10 |
| 15. ~ q |
MT : 12,14 |
| 16. ~ ( q |
OA : 6,14 |
| 17. q |
NI : 16 |
| 18. q |
OK : 17 |
| 19. ~ r Odp. Sprzecznosc: 13, 19 ; 15,18 - tautologia. _____ |
OK : 17 |
| l) {~(sVr) |
|
| 1. ~(s V r) |
zal. |
| 2. ~ [(q |
z.d.n. |
| 3. ~ (q |
NA : 2 |
| 4. ~ (q |
OK : 3 |
| 5. ~ (s V r) |
OK : 3 |
| 6. ~ [(s |
RO :1,5 |
| 7.q |
NI : 4 |
| 8. ~ s |
NA : 5 |
| 9. (s |
NI : 6 |
| 10. q | OK : 7 |
| 11. ~ p | OK : 7 |
| 12. ~ s | OK : 8 |
| 13. ~ r |
OK : 8 |
| 14. s |
OK : 9 |
| 15.~ (p V ~ r) |
OK : 9 |
| 16. ~ p |
NA : 15 |
| 17. ~ p |
OK : 16 |
| 18. ~ ~ r | OK : 16 |
| 19. r Odp. Sprzecznosc: 13, 19 - schemat to tautologia. |
ON : 18 |
|
|
||
| Copyright (C) 1997 - 2014 by Roman Mazur |
[ przykładowe wpisy ]