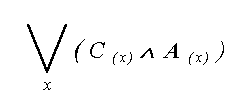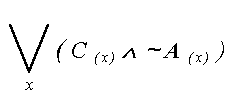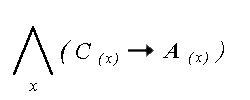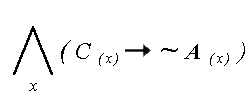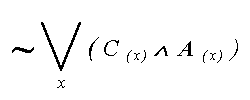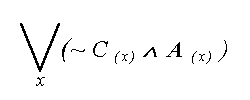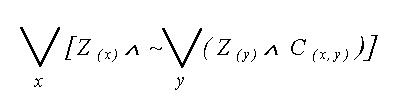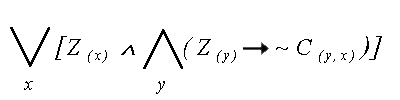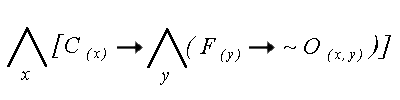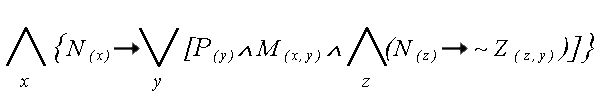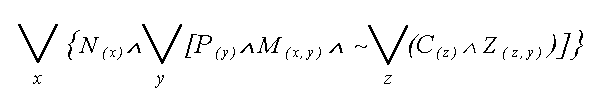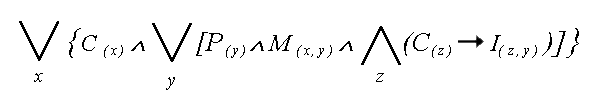Logika u podstaw... => RACHUNEK KWANTYFIKATOROW

Roman Mazur: Logika u podstaw...

Logika u podstaw...
---- Księga Gości ----
Wpisz się... | Przeglądaj...

LOGIKA - ĆWICZENIA [RACHUNEK KWANTYFIKATORÓW - rachunek predykatów pierwszego rzędu] SCHEMATY KWANTYFIKATOROWE

1. Logika u podstaw - ZDANIE i SPOJNIKI ...____

2. Logika u podstaw - WARTOSC LOGICZNA __

3. Logika u podstaw - EKSTENSJONALNOSC i ...

4. Logika u podstaw - TAUTOLOGIA i KONTR..._

5. Logika u podstaw - SYSTEM_ZALOZENIOWY

6. Logika u podstaw - PRAWDA LOGICZNA ___

7. Logika u podstaw - WYNIKANIE LOGICZNE _

8. Logika u podstaw - ROWNOWAZNOSC ...___

9. Logika u podstaw - WNIOSKOWANIE ..._____

10. Logika u podstaw - FALSZ LOGICZNY_ ___

11. Logika u podstaw - SPRZECZNY ZBIOR ..._

12. Logika u podstaw - KWANTYFIKATORY ..._
_______________________________________
______strona domowa logiki u podstaw_____

12. KWANTYFIKATORY - sa to najzwyczajniejsze w swiecie stale (oczywiscie logiczne), wystepujace sobie w (noszacym znamiona graficznego rozpisu sensu zdania) rachunku kwantyfikatorow, a oznaczane przez wiecej niz wielu wytrawnych Logikow w nastepujacy sposob:

- KWANTYFIKATOR DUZY (ogólny) - ostatnimi czasy zapisywany jako "FOR ALL":
(czytany: “DLA KAZDEGO...”)

- KWANTYFIKATOR MALY (egzystencjalny) - ostatnio zapisywany jako "THERE EXISTS":
(czytany: “ISTNIEJE TAKI ..., ZE")

NAZWY- sa dowolne zmienne - pojedyncze rzeczy, wystepujace w zdaniu i oznaczamy je malymi literami w nastepujacy sposob :

" x , y , z... "

PREDYKATY - sa to zmienne - wlasnosci NAZW i relacje miedzy tymi NAZWAMI zachodzace. Oznaczamy je wielkimi literami:

" P , Q , R , S... "

Predykaty reprezentuja w wyrazeniu rachunku kwantyfikatorow albo NAZWE (zapisuje sie to zawsze tak: P_{(
x )}), albo tez relacje pomiedzy NAZWAMI ( zapis : P_{(
x , y )}).

SCHEMAT ZDANIOWY - jest to symboliczny zapis odzwierciedlajacy zawartosc zdania, np.: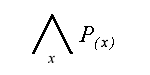

(CZYTAJ : “Dla kazdego x , x jest Ptakiem.” )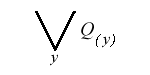

(CZYTAJ : “Istnieje taki y , ze y jest Qra.” )

"NO I ZACZELY SIE SCHODY...?!" ;-)

A w zadnym razie - bo nie ma przeciez dla naszych logika niejednokrotnie juz "skalanych" umyslow rzeczy niepojetych! Takze i te "straszne", na pierwszy rzut oka, “Stwory - Kwantyfikatory”, sa w istocie “lagodnymi i najlogiczniejszymi w tej czesci Galaktyki istotami nieozywionymi”, bez wzgledu na to, co mialoby to oznaczac...

Trzeba nam first zapamietac ktory symbol odnosi sie do ktorego kwantyfikatora. Ulatwimy to sobie - "lotem blyskawicy" przy-
swoimy te informacje, otrzymujac ku temu wydatna pomoc specjalisty w polu kwantyfikatorow - gromowladnego Zeusa:

KWANTYFIKATOR DUZY - “DLA KAZDEGO...”

KWANTYFIKATOR MALY - “ISTNIEJE TAKI ... , ZE ...”

Kolejna czynnoscia bedzie zapamietanie reguly tworzenia schematow kwantyfikatorowych. Ta rzecz przedstawia sie tak :

I PRZYKLAD

Domagajac sie w zamian schematu kwantyfikatorowego, obdarowano nas zdaniem:

“Kubus widzial Antykubusia, goniacego czas.”

- wypisujemy sobie zmienne nazwowe (NAZWY), ktorymi sa zawsze tylko te wszystkie podmioty (rzeczowniki) , w stosunku do ktorych inne czesci zdania (moga nimi byc takze rzeczowniki w formie dopelnienia), pelnia funkcje opisowa:

x - Kubus
y - Antykubus
z - czas

- dalej powinnoscia nasza jest utworzenie zmiennych predykatowych (PREDYKATOW), ktorymi sa zawsze:

1. - informacje o wystepowaniu podmiotu w zdaniu (PREDYKATY JEDNOARGUMENTOWE - bo jedna zmienna w nawiasie);

2. - te czesci zdania, ktore wystepuja pomiedzy NAZWAMI, laczac je ze soba w spojna calosc (PREDYKATY DWUARGUMENTOWE - bo dwie zmienne w nawiasie):

OBA RODZAJE WYSTEPUJA ZAWSZE W FORMIE TWIERDZACEJ !

K _{( x )} - x jest Kubusiem A _{( y )} - y jest Antykubusiem C _{( z )} - z jest czasem	(TYCH JEST ZAWSZE TYLE, ILE NAZWZNALEZLISMY W BADANYM ZDANIU)
W _{( x , y )} - x widzial y G _{( y , z )} - y gonil z	(TYCH JEST O JEDEN MNIEJ, NIZ ILOSC NAZW W BADANYM ZDANIU)

Dla jeszcze lepszego uchwycenia watku, wyobraz sobie dlon:

Widzisz wyraznie, ze predykatow jednoargumentowych mamy trzy (wyprostowane palce : wskazujacy, duzy i serdecz-
ny), natomiast predykaty dwuargumentowe sa dwa (przestrzenie miedzypalcowe, laczace trzy powyzsze palce ze soba).

- nastepnie przeksztalcmy sobie nasze zdanie tak, aby przybralo forme ulatwiajaca nam dopasowanie odpowiednich kwantyfikatorow :

“(Jeden) Kubus widzial (jednego) Antykubusia, goniacego (jeden) czas.”

Mamy teraz pewnosc, ze :

a) Kubus jest jeden, wiec mozemy powiedziec : “Istnieje taki x , ze x jest Kubusiem” i zapisac to zaraz w schemacie, uzywajac w tym celu MALEGO kwantyfikatora.

b) Antykubus jest jeden, wiec mozemy powiedziec : “Istnieje taki y , ze y jest Antykubusiem” i zapisac to zaraz w schemacie, uzywajac w tym celu MALEGO kwantyfikatora.

c) czas jest jeden, wiec mozemy powiedziec: “Istnieje taki z , ze z jest czasem” i zapisac to zaraz w schemacie, uzywajac w tym celu MALEGO kwantyfikatora.

- przystepujemy wiec do zapisania naszego zdania w postaci schematu kwantyfikatorowego :

W uproszczeniu wyglada to tak :

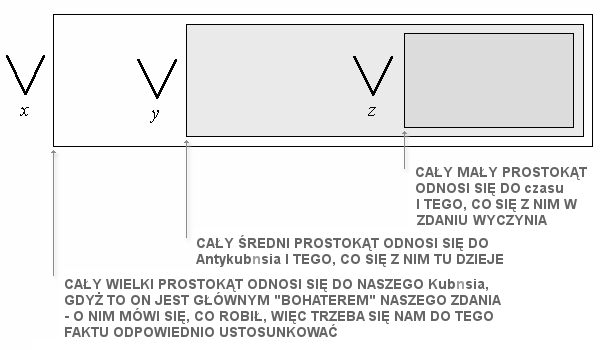A powstal on w nastepujacy sposob :

- ustalilismy, ze glowna NAZWA w tym zdaniu jest Kubus, bo mowi sie tu, co jemu wlasnie sie przytrafilo, wiec rozpoczynamy od napisania tego, ze Kubus istnieje (przynajmniej w naszym zdaniu) :

UWAGA! Czyta sie to tak: “Istnieje taki x, ze x jest Kubusiem...” PAMIETAJ !

- nastepnie zaznaczamy w schemacie istnienie kolejnej NAZWY, ktora jest wobec Kubusia podrzedna (to Kubus ma z nia do czynienia i gdyby nie on, nie wiedzielibysmy wcale o jej istnieniu) :

“Istnieje taki x, ze x jest Kubusiem i istnieje taki y, ze y jest Antykubusiem...”

UWAGA! ISTNIEJE NIEPISANA ZASADA (KTORA ZAPEWNE NIE TYLKO TU UDALO SIE ODKRYC), W MYSL KTOREJ TA KONIUNKCJA (NADAJACA SCHEMATOWI W TYM MIEJSCU SPOJNOSCI), JEST NIEODLACZNA TOWARZYSZKA ZYCIA MALEGO KWANTYFIKATORA - TZN, ZE GDY PISZEMY MALY KWANTYFIKATOR,
TO - W PRYZMACIE LOGIKI-KLASYKI DWUWARTOSCIOWEJ - OBOJETNIE CO BY SIE NIE DZIALO WE WSZECHSWIECIE, ZAWSZE (PRZY BUDOWANIU SCHEMATU KWANTYFIKATOROWEGO ZDANIA INFORMUJACEGO O JAKICHS FAKTACH), UZYSKUJE SIE SPOJNOSC Z RESZTA ZAPISYWANYCH
RZECZY POPRZEZ "AUTOMATYCZNE" ZASTOSOWANIE W ODP. MSC. SYMBOLU KONIUNKCJI. PAMIETAJ!

- teraz uwzgledniamy stosunek panujacy miedzy pierwsza i druga NAZWA, pamietajac, zeby zastosowac ku temu symbol koniunkcji, gdyz ostatnim wpisanym przez nas kwantyfikatorem byl maly kwantyfikator :

“Istnieje taki x, ze x jest Kubusiem i istnieje taki y, ze y jest Antykubusiem i x widzial y...”

- kolejny krok to koniecznosc przedstawienia w schemacie kolejnego bohatera naszego zdania - czasu, ktory jest tu nierozlacznie zwiazany z Antykubusiem - to on figluje z nim. Pamietamy oczywiscie o symbolu koniunkcji, laczacym istnienie tej NAZWY z tym, co dotad napisalismy

“Istnieje taki x, ze x jest Kubusiem i istnieje taki y, ze y jest Antykubusiem i x widzial y i istnieje taki z, ze z jest czasem...”

- no i nie pozostalo nam nic innego, jak dopelnienie schematu relacja zachodzaca pomiedzy Antykubusiem i czasem - “y gonil z”, jak zwykle wpisujac w odpowiednim miejscu symbol koniunkcji, bo determinuje to maly kwantyfikator :

“Istnieje taki x, ze x jest Kubusiem i istnieje taki y, ze y jest Antykubusiem i x widzial y i istnieje taki z, ze z jest czasem i y gonil z.”

Podsumowujac, cala praca powinna wygladac nastepujaco :

“Kubus widzial Antykubusia, goniacego czas.”
[ “(Jeden) Kubus widzial (jednego) Antykubusia, goniacego (jeden) czas.” ]

x - Kubus
y - Antykubus
z - czas

K _{( x )} - x jest Kubusiem
A _{( y )} - y jest Antykubusiem
C _{( y )} - z jest czasem

W _{( x , y )} - x widzial y
G _{( y , z )} - y gonil z

“Istnieje taki x, ze x jest Kubusiem i istnieje taki y, ze y jest Antykubusiem i x widzial y i istnieje taki z, ze z jest czasem i y gonil z.”

II PRZYKLAD

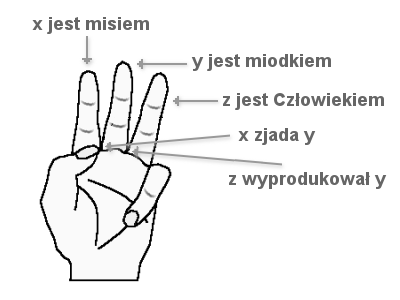
Tym razem dostalismy takie zdanie :

“Wszystkie misie nie zjedza miodku, wyprodukowanego przez Czlowieka .”

- wypisujemy zmienne nazwowe (NAZWY), ktorymi sa zawsze te wszystkie podmioty (rzeczowniki) , w stosunku do ktorych inne czesci zdania (moga nimi byc takze rzeczowniki w formie dopelnienia), pelnia funkcje opisowa :

x - mis
y - miodek
z - Czlowiek

- dalej tworzymy (na poczatku "na dloni") zmienne predykatowe (PREDYKATY), ktorymi sa zawsze:

1. - informacje o wystepowaniu podmiotu w zdaniu (PREDYKATY JEDNOARGUMENTOWE - bo jedna zmienna w nawiasie) ;

2. - te czesci zdania, ktore wystepuja pomiedzy NAZWAMI, laczac je ze soba w spojna calosc (PREDYKATY DWUARGUMENTOWE - bo dwie zmienne w nawiasie):

M _{( x )} - x jest misiem
UWAGA ! Mimo, ze w zdaniu sa “misie” - slowo informujace o zbiorowym charakterze wystepujacej tu nazwy, my umieszczamy w predykacie ZAWSZE nazwe w formie liczby pojedynczej : “mis”. PAMIETAJ !
U _{( y )} - y jest miodkiem
C _{( z )} - z jest Czlowiekiem
Z _{( x , y )} - x zjada y
W _{( z , y )} - z wyprodukowal y

- nastepnie przeksztalcamy zdanie tak, aby przybralo forme ulatwiajaca nam dopasowanie odpowiednich kwantyfikatorow:

“Dla kazdego misia nie istnieje taki (jeden) miodek, ktory nadawalby sie do zjedzenia i zostalby wyprodukowany przez (jednego) Czlowieka .”

Mamy teraz pewnosc, ze:

a) “mis” wystepowac bedzie w schemacie z DUZYM kwantyfikatorem.

b) “miodek” jest jeden - wystepowac bedzie w schemacie z MALYM kwantyfikatorem.

c) “Czlowiek” jest jeden, wiec powiemy : “Istnieje taki z , ze z jest Czlowiekiem” i zapiszemy to, uzywajac MALEGO kwantyfikatora.

- nasze zdanie w postaci schematu kwantyfikatorowego:

W uproszczeniu wyglada to tak :

A powstal on w nastepujacy sposob :

- ustalilismy, ze glowna NAZWA w tym zdaniu jest “mis”, bo mowi sie tu, co jemu (wlasciwie im - mamy liczbe mnoga ), sie przytrafia, wiec rozpoczynamy od napisania faktu, ze to, co tu dzieje sie, dotyczy kazdego misa :

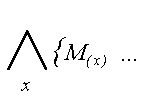UWAGA! Czyta sie to tak: “Dla kazdego x, x jest misiem...” PAMIETAJ !
- teraz kolejna NAZWA, ktora jest wobec misia podrzedna :

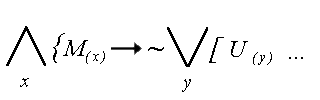“Dla kazdego x, x jest misiem, to NIE istnieje taki y, ze y jest miodkiem..."
UWAGA! KOLEJNA NIEPISANA ZASADA (KTORA TEZ ZAPEWNE NIE TYLKO TU UDALO SIE ODKRYC), W MYSL KTOREJ TA IMPLIKACJA (NADAJACA SCHEMATOWI W TYM MIEJSCU SPOJNOSCI), JEST NIEODLACZNA TOWARZYSZKA ZYCIA DUZEGO KWANTYFIKATORA - TZN, ZE GDY PISZEMY DUZY KWANTYFIKATOR, TO - W PRYZMACIE LOGIKI-KLASYKI DWUWARTOSCIOWEJ - OBOJETNIE CO BY SIE NIE DZIALO WE WSZECHSWIECIE, ZAWSZE (PRZY BUDOWANIU SCHEMATU KWANTYFIKATOROWEGO ZDANIA INFORMUJACEGO O JAKICHS FAKTACH), UZYSKUJE SIE SPOJNOSC Z RESZTA ZAPISYWANYCH RZECZY POPRZEZ "AUTOMATYCZNE" ZASTOSOWANIE W ODP. MSC. SYMBOLU IMPLIKACJI. PAMIETAJ!
- teraz relacja zachodzaca miedzy pierwsza i druga NAZWA, pamietamy, zeby zastosowac symbol koniunkcji, gdyz ostatnim wpisanym przez nas kwantyfikatorem byl maly kwantyfikator :

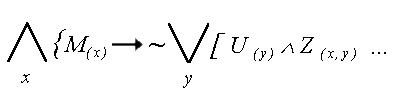“Dla kazdego x, x jest misiem, to NIE istnieje taki y, ze y jest miodkiem i x zjada y..." - przedstawiamy w schemacie kolejnego bohatera naszego zdania - Czlowieka, ktory jest tu nierozlacznie zwiazany z miodkiem . Pamietamy oczywiscie o symbolu koniunkcji, laczacym istnienie tej NAZWY z tym, co dotychczas napisalismy (ostatnio wpisalismy maly kwantyfikator):

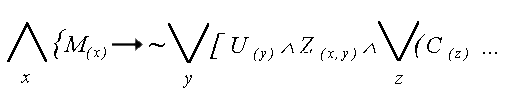“Dla kazdego x, x jest misiem, to NIE istnieje taki y, ze y jest miodkiem i x zjada y, i istnieje taki z, ze z jest Czlowiekiem..." - dopelniamy schemat relacja zachodzaca pomiedzy Czlowiekiem i miodkiem - “z wyprodukowal y”, jak zwykle wpisujac w odpowiednim miejscu symbol koniunkcji, bo determinuje to ostatni maly kwantyfikator :

“Dla kazdego x, x jest misiem, to NIE istnieje taki y, ze y jest miodkiem i x zjada y, i istnieje taki z, ze z jest Czlowiekiem, i z wyprodukowal y." Podsumowujac, cala praca powinna wygladac nastepujaco : “Wszystkie misie nie zjedza miodku, wyprodukowanego przez Czlowieka .” [ “Dla kazdego misia nie istnieje taki (jeden) miodek, ktory nadawalby sie do zjedzenia i zostalby wyprodukowany przez (jednego) Czlowieka .” ] x - mis y - miodek z - Czlowiek M _{( x )}- x jest misiem U _{( y )} - y jest miodkiem C _{( z )} - z jest Czlowiekiem Z _{( x , y )} - x zjada y W _{( z , y )} - z wyprodukowal y

"Dla kazdego x, jezeli x jest misiem, to NIE istnieje taki y, ze y jest miodkiem i x zjada y, i istnieje taki z, ze z jest Czlowiekiem i z wyprodukowal y.”

CWICZENIE 19 I Cwiczenie do rozdzialu nr 12 I

To bedzie juz ostatnie, ale za to chyba najbardziej spektakularne z tutejszych cwiczen... ;)
Wykonamy tu sobie rzecz zapewne niepojeta dla nas samych - tyle ze tych z przeszlosci,
kiedy to nie snilo sie “im - nam” nawet, ze cos takiego, jak schematy kwantyfikatorowe w ogole istnieje,
a co dopiero mowic o ich samodzielnym konstruowaniu! Nim przystapimy do rzeczy, chce podziekowac
Ci za spedzenie "w tych stronach" - credo - wartosciowych chwil dla Twojego umyslu, i co za tym idzie dla Twojej przyszlosci... No to pozdrawiam szare komorki, ale nim to, poprosze o zaprzegniecie ich "ponizej" jeszcze raz:
"DO DZIELA!" :)

a) “Istnieja Ludzie, ktorzy sa Aniolami.”
[ mówiąc w uproszczeniu: “Istnieje taka (przynajmniej jedna) istota, ktora jest jednoczesnie Czlowiekiem i Aniolem.” ]

x - istota
C _{( x )} - x jest Czlowiekiem
A _{( x )} - x jest Aniolem

- Maly kwantyfikator, bo zdanie nie mowi o wszystkich Ludziach, ale o niektorych z nich.
- Koniunkcja, bo to nieodlaczna towarzyszka malego kwantyfikatora.
- W obu nawiasach “x”, bo w tym przypadku chodzi o jedna i ta sama istote, ktora jest jednoczesnie Czlowiekiem i Aniolem.

“Istnieje taki x, ze x jest Czlowiekiem i x jest Aniolem.”
_____

b) “Istnieja Ludzie, ktorzy nie sa Aniolami.”
[ mówiąc w uproszczeniu: “Istnieje taka (przynajmniej jedna) istota, ktora jest Czlowiekiem i nie jest Aniolem.” ]

x - istota
C _{( x )} - x jest Czlowiekiem
A _{( x )} - x jest Aniolem

“Istnieje taki x, ze x jest Czlowiekiem i x nie jest Aniolem.”
_____

c) “Wszyscy Ludzie sa Aniolami.”
[ mówiąc w uproszczeniu: “Kazda istota, ktora jest Czlowiekiem, jest jednoczesnie Aniolem.” ]

x - istota
C _{(
x )} - x jest Czlowiekiem
A _{(
x )} - x jest Aniolem

- Duzy kwantyfikator, bo zdanie mowi o wszystkich Ludziach.
- Implikacja, bo to nieodlaczna towarzyszka duzego kwantyfikatora.
- W obu nawiasach “x”, bo w tym przypadku chodzi o wszystkie i te same istoty, ktore sa jednoczesnie ludzmi i Aniolami.

“Dla kazdego x, jezeli x jest Czlowiekiem, to x jest Aniolem.”
_____

d) “Zaden Czlowiek nie jest Aniolem.”
[ mówiąc w uproszczeniu: WARIANT I - "Kazda istota, ktora jezeli jest Czlowiekiem, to nie jest Aniolem.”
lub też: WARIANT II - "Nie istnieje istota, ktora jest zarazem Czlowiekiem i Aniolem.” ]

x - istota
C _{( x
)} - x jest Czlowiekiem
A _{( x
)} - x jest Aniolem

WARIANT I	WARIANT II
“Dla kazdego x, jezeli x jest Czlowiekiem, to x nie jest Aniolem.”	“Nie istnieje taki x, ze x jest Czlowiekiem i x jest Aniolem.”

_____

e) “Tylko Ludzie sa Aniolami.”
[ mówiąc w uproszczeniu: “Kazda istota, ktora jesli jest Czlowiekiem, to jest jednoczesnie Aniolem.” ]

x - istota
C _{( x
)} - x jest Czlowiekiem
A _{( x
)} - x jest Aniolem

“Dla kazdego x, jezeli x jest Czlowiekiem, to x jest Aniolem.”
_____

f) “Nie tylko Ludzie sa Aniolami.”
[ mówiąc w uproszczeniu: “Istnieje taka (przynajmniej jedna) istota, ktora nie jest Czlowiekiem i jest Aniolem.” ]

x - istota
C _{( x
)} - x jest Czlowiekiem
A _{( x
)} - x jest Aniolem

- Maly kwantyfikator, bo zdanie nie mowi o wszystkich istotach, ale o niektorych z nich.
- Koniunkcja, bo to nieodlaczna towarzyszka malego kwantyfikatora.
- W obu nawiasach “x”, bo w tym przypadku chodzi o jedna i ta sama istote, ktora NIE jest jednoczesnie Czlowiekiem, ale jest Aniolem.

“Istnieje taki x, ze x nie jest Czlowiekiem i x jest Aniolem.”
_____

g) “Kazda Polka jest corka jakiejs Europejki.”
[ mówiąc w uproszczeniu: “Dla kazdej Polki istnieje taka (przynajmniej jedna) Europejka, dla ktorej ona jest corka.” ]

x - Polka
y - Europejka
Z _{( x
)}- x jest Polka
Z _{( y
)} - y jest Europejka
C_{(
x
,
y )} - x jest corka y

- Duzy kwantyfikator, bo w zdaniu chodzi o kazda, bez wyjatku, Polke.
- Implikacja, bo pobliskim kwantyfikatorem (z lewej str.), byl duzy kwantyfikator.
- Nastepnie maly kwantyfikator, bo trzeba nam uwzglednic istnienie w naszym zdaniu kolejnej NAZWY.
- Koniunkcja, bo wyznacza to lezacy z lewej strony maly kwantyfikator.

“Dla kazdego x, jezeli x jest Polka, to istnieje taki y, ze y jest Europejka i x jest corka y.”
_____

h) “Pewna Polka nie jest corka zadnej Europejki.”
[ mówiąc w uproszczeniu: “Istnieje taka Polka, ze nie istnieje inna (przynajmniej jedna) Europejka, ktorej ona jest corka.” ]

x - Polka
y - Europejka
Z _{( x
)}- x jest Polka
Z _{( y
)} - y jest Europejka
C _{( x
, y )} - x jest corka y

- Maly kwantyfikator, bo w zdaniu chodzi o jedna Polke.
- Koniunkcja, bo najblizszym kwantyfikatorem (z lewej strony), byl maly kwantyfikator.
- Drugi maly kwantyfikator, bo trzeba nam uwzglednic NIE istnienie nawet jednej Europejki, ktora bylaby matka Bohaterki.
- Koniunkcja, bo wyznacza to lezacy z lewej strony maly kwantyfikator.

“Istnieje taki x, ze x jest Polka, i nie istnieje taki y, ze y jest Europejka i x jest corka y.”
_____

i) “Pewna Europejka nie ma corki posrod Polek.”
[ mówiąc w uproszczeniu: “Istnieje taka Europejka, ze kazda Polka nie jest jej corka.” ]

x - Europejka
y - Polka
Z _{( x
)}- x jest Europejka
Z _{( y
)} - y jest Polka
C _{( y
, x )} - y jest corka x

“Istnieje taki x, ze x jest Europejka, i dla kazdego y, jezeli y jest Polka, to y nie jest corka x.”
_____

j) “Pewien Medrzec nie obejrzal zadnego filmu.”
[ mówiąc w uproszczeniu: “Istnieje taki Medrzec, ktory nie obejrzal zadnego z wszystkich filmow.” ]

x - Medrzec
y - film
M _{( x
)} - x jest Medrcem
F _{( y
)} - y jest filmem
O _{( x
, y )} - x obejrzal y

“Istnieje taki x, ze x jest Medrcem, i dla kazdego y, jezeli y jest filmem, to x nie obejrzal y.”
_____

k) “Pewien Czlowiek nie ma Sasiada.”
[ mówiąc w uproszczeniu: "Istnieje taki Czlowiek, ktory nie ma zadnego Sasiada.” ]
W schemacie sformulujemy czesc zdania tak :“nie istnieje (nawet jeden) Sasiad.”

x - Czlowiek
y - Czlowiek
C _{( x
)} - x jest Czlowiekiem
C _{( y
)} - y jest Czlowiekiem
S _{( y
, x )} - y jest Sasiadem x

“Istnieje taki x, ze x jest Czlowiekiem, i nie istnieje taki y, ze y jest Czlowiekiem i y jest Sasiadem x.”
_____

l) “Wszyscy Ludzie sa Sasiadami wszystkich.”
[ mówiąc w uproszczeniu: “Kazdy Czlowiek, jest Sasiadem kazdego Czlowieka.” ]

x - Czlowiek
y - Czlowiek
C _{( x
)} - x jest Czlowiekiem
C _{( y
)} - y jest Czlowiekiem
S _{( y
, x )} - y jest Sasiadem x

“Dla kazdego x, jesli x jest Czlowiekiem, to kazdy y, jezeli y jest Czlowiekiem, to y jest Sasiadem x.”
_____

m) “Nikt nie ma Sasiada."
[ mówiąc w uproszczeniu: ”Nie istnieje taki Czlowiek, ktory nie ma zadnego Sasiada.” ]

x - Czlowiek
y - Czlowiek
C _{( x
)} - x jest Czlowiekiem
C _{( y
)} - y jest Czlowiekiem
S _{( y
, x )} - y jest Sasiadem x

“Nie istnieje taki x, ze x jest Czlowiekiem, i nie istnieje taki y, ze y jest Czlowiekiem i y nie jest Sasiadem x.”
_____

n) “Wszyscy przeczytali jakas ksiazke."
[ mówiąc w uproszczeniu: ”Kazdy Czlowiek, przeczytal (przynajmniej jedna) ksiazke.” ]

x - Czlowiek
y - ksiazka
C _{( x
)} - x jest Czlowiekiem
F _{( y
)} - y jest ksiazka
O _{( x
, y )} - x przeczytal y

“Dla kazdego x, jezeli x jest Czlowiekiem, to istnieje taki y, ze y jest ksiazka i x przeczytal y.”
_____

o) “Jest film, ktorego nie obejrzeli wszyscy Ludzie.”
[ mówiąc w uproszczeniu: “Istnieje taki film, ktorego nie obejrzal kazdy Czlowiek.” ]

x - film
y - Czlowiek
F _{( x
)} - x jest filmem
C _{( y
)} - y jest Czlowiekiem
O _{( y
, x )} - y obejrzal x

“Istnieje taki x, ze x jest filmem, i dla kazdego y, jezeli y jest Czlowiekiem, to y nie obejrzal x.”
_____

p) “Zaden z nas nie przeczytal wszystkich ksiazek.”
[ mówiąc w uproszczeniu: “Kazdy Czlowiek nie przeczytal kazde ksiazki.” ]

x - Czlowiek
y - ksiazka
C _{( x
)} - x jest Czlowiekiem
F _{( y
)} - y jest ksiazka
O _{( x
, y )} - x przeczytal y

“Dla kazdego x, jesli x jest Czlowiekiem, to kazdy y, jezeli y jest ksiazka, to x nie przeczytal y.”
_____

q) “Wszyscy Naukowcy maja poglady, z ktorymi wszyscy Naukowcy sie nie zgadzaja.”
[ mówiąc w uproszczeniu: “Kazdy Naukowiec ma (przynajmniej jeden) poglad, z ktorym inni (kazdy) Naukowcy sie nie zgadzaja.” ]

x - Naukowiec
y - poglad
z - Naukowiec
N _{( x
)} - x jest Naukowcem
P _{( y
)} - y jest pogladem
N _{( z
)} - z jest Naukowcem
M _{( x
, y )} - x ma y
Z _{( z
, y )} - z zgadza sie z y

“Dla kazdego x, jesli x jest Naukowcem, to istnieje taki y, ze y jest pogladem i x ma y, i dla kazdego z, jezeli z jest Naukowcem, to z nie zgadza sie z y.”

- Duzy kwantyfikator, bo w zdaniu chodzi o kazdego Naukowca.
- Maly kwantyfikator, bo uwzgledniamy istnienie przynajmniej jednego pogladu, ktory nalezy do wszystkich Naukowcow (kazdy ma oczywiscie swoj wlasny).
- Koniunkcja, bo wyznacza to lezacy z lewej strony maly kwantyfikator.
- Duzy kwantyfikator, bo informujemy o tym, ze wszyscy Naukowcy, jak jeden maz, nie zgadzaja sie z czyms, co twierdzi na jakis temat kazdy (inny), z nich.
- Implikacja (po duzym kwantyfikatorze), bo jesli z jest Naukowcem, to wg naszego zdania, “w genach nosi brak akceptacji dla choc jednego sadu innych Naukowcow.”
_____

r) “Pewni Naukowcy maja poglady, z ktorymi zaden Czlowiek sie nie zgadza.”
[ czyli: “Istnieje taki (przynajmniej) jeden Naukowiec, ktory ma (przynajmniej) jeden poglad, z ktorym ani jeden Czlowiek sie nie zgadza.” ]

x - Naukowiec
y - poglad
z - Czlowiek
N _{( x
)} - x jest Naukowcem
P _{( y
)} - y jest pogladem
C _{( z
)} - z jest Naukowcem
M _{( x
, y )} - x ma y
Z _{( z
, y )} - z zgadza sie z y

“Istnieje taki x, ze x jest Naukowcem i istnieje taki y, ze y jest pogladem, i x ma y, i nie istnieje taki z, ze z jest Czlowiekiem, i z zgadza sie z y.”

- Maly kwantyfikator, bo w zdaniu chodzi o przynajmniej jednego Naukowca.
- Maly kwantyfikator, bo uwzgledniamy istnienie przynajmniej jednego pogladu, ktory nalezy do tego jednego Naukowca.
- Negacja malego kwantyfikatora, bo “NIE istnieje pod Sloncem nawet jedna Osoba, ktora z tym konkretnym pogladem zgodzilaby sie”.
_____

s) “Pewien Czlowiek ma przekonania, z ktorymi identyfikuja sie wszyscy Ludzie.”
[ mówiąc w uproszczeniu: “Istnieje taki Czlowiek, ktory ma (przynajmniej jedno) przekonanie, z ktorym identyfikuje sie kazdy Czlowiek.” ]

x - Czlowiek
y - przekonanie
z - Czlowiek
C _{( x
)} - x jest Czlowiekiem
P _{( y
)} - y jest przekonaniem
C _{( z
)} - z jest Czlowiekiem
M _{( x
, y )} - x ma y
I _{( z
, x )} - z identyfikuje sie z y

“Istnieje taki x, ze x jest Czlowiekiem, i istnieje taki y, ze y jest przekonaniem, i x ma y, i dla kazdego z, jezeli z jest Czlowiekiem, to z identyfikuje sie z y.”
_____

t) “Sa ubrania stworzone przez Dyktatorow mody, ktorzy nie sa pozbawieni zmyslu uzytkowosci.”
[ inaczej mowiac: "Istnieje takie (przynajmniej) jedno ubranie, ktore zostalo stworzone przez (przynajmniej) jednego Dyktatora mody, ktorym nie jest pozbawiony (jednego) zmyslu uzytkowosci.” ]

x - ubranie
y - Dyktator mody
z - cecha
U _{( x )} - x jest ubraniem
D _{( y
)} - y jest Dyktatorem mody
P _{( z
)} - z jest zmyslem uzytkowosci
K _{( y
, x )} - y stworzyl x
N _{( y
, z )} - y jest pozbawiony z

“Istnieje taki x, ze x jest ubraniem i istnieje taki y, ze y jest Dyktatorem mody, i y stworzyl x, i nie istnieje taki z, ze z jest zmyslem uzytkowosci, i y jest pozbawiony z.”
_____

u) “Zaden Czlowiek nie zniszczy bezzasadnie Istoty, ktora ma w sobie wszystkie pierwiastki zycia.”
[ czyli: "Nie istnieje taki Czlowiek, ktory zniszczy bezzasadnie (jedna) Istote, ktora ma w sobie kazdy pierwiastek zycia." ]

x - Czlowiek
y - Istota
z - symptom
C _{( x
)} - x jest Czlowiekiem
I _{( y
)} - y jest Istota
P _{( z
)} - z jest pierwiastkiem zycia
Z _{( x
, y )} - x zniszczy bezzasadnie y
M _{( y
, z )} - y ma w sobie z

“Nie istnieje taki x, ze x jest Czlowiekiem i istnieje taki y, ze y jest Istota, i x zniszczy bezzasadnie y, i dla kazdego z, jezeli z jest pierwiastkiem zycia, to y ma w sobie z.”

[ przykładowe wpisy ]